How ranking works
Articles are scored based on their upvote score, the time since the article was submitted, and various penalties using the following formula: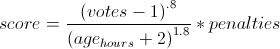 Because the time has a larger exponent than the votes, an article's score will eventually drop to zero, so nothing stays on the front page too long. This exponent is known as gravity.
You might expect that every time you visit Hacker News, the stories are scored by the above formula and sorted to determine their rankings. But for efficiency, stories are individually reranked only occasionally. When a story is upvoted, it is reranked and moved up or down the list to its appropriate spot, leaving the other stories unchanged. Thus, the amount of reranking is significantly reduced. There is, however, the possibility that a story stops getting votes and ends up stuck in a high position. To avoid this, every 30 seconds one of the top 50 stories is randomly selected and reranked. The consequence is that a story may be "wrongly" ranked for many minutes if it isn't getting votes.
In addition, pages can be cached for 90 seconds.
Because the time has a larger exponent than the votes, an article's score will eventually drop to zero, so nothing stays on the front page too long. This exponent is known as gravity.
You might expect that every time you visit Hacker News, the stories are scored by the above formula and sorted to determine their rankings. But for efficiency, stories are individually reranked only occasionally. When a story is upvoted, it is reranked and moved up or down the list to its appropriate spot, leaving the other stories unchanged. Thus, the amount of reranking is significantly reduced. There is, however, the possibility that a story stops getting votes and ends up stuck in a high position. To avoid this, every 30 seconds one of the top 50 stories is randomly selected and reranked. The consequence is that a story may be "wrongly" ranked for many minutes if it isn't getting votes.
In addition, pages can be cached for 90 seconds.
Raw scores and the #1 spot on a typical day
The following image shows the raw scores (excluding penalties) for the top 60 HN articles throughout the day of November 11. Each line corresponds to an article, colored according to its position on the page. The red line shows the top article on HN. Note that because of penalties, the article with the top raw score often isn't the top article.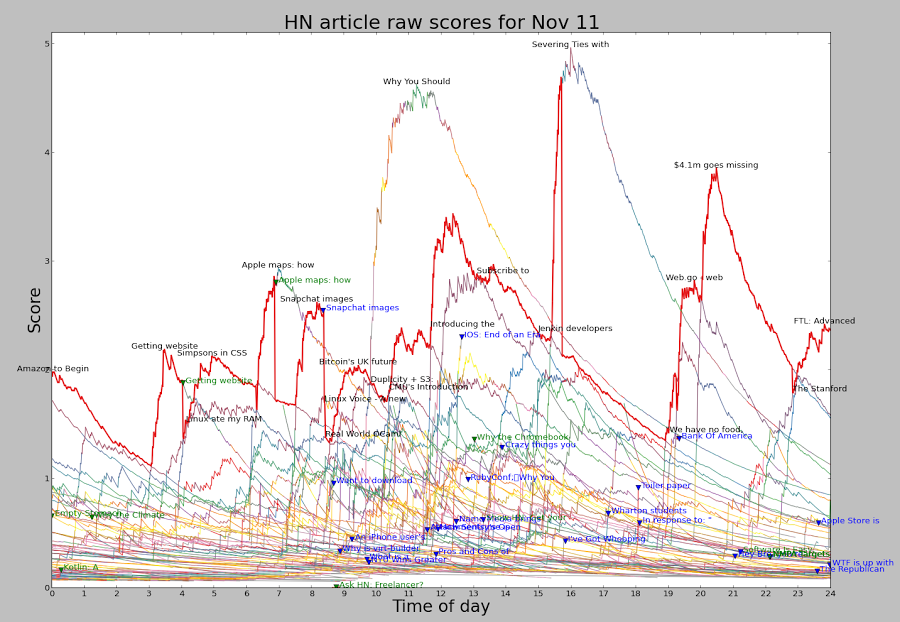 This chart shows a few interesting things. The score for an article shoots up rapidly and then slowly drops over many hours. The scoring formula accounts for much of this: an article getting a constant rate of votes will peak quickly and then gradually descend. But the observed peak is even faster - this is because articles tend to get a lot of votes in the first hour or two, and then the voting rate drops off. Combining these two factors yields the steep curves shown.
There are a few articles each day that score much above the rest, along with a lot of articles in the middle. Some articles score very well but are unlucky and get stuck behind a more popular article. Other articles hit #1 briefly, between the fall of one and the climb of another.
Looking at the difference between the article with the top raw score (top of the graph) and the top-ranked article (red line), you can see when penalties have been applied.
The article Getting website registration completely wrong hit #1 early in the morning, but was penalized for controversy and rapidly dropped down the page, letting Linux ate my RAM briefly get the #1 spot before Simpsons in CSS overtook it.
A bit later, the controversy penalty was applied to Apple Maps shortly after it reached the #1 spot, causing it to lose its #1 spot and rapidly drop down the rankings.
The Snapchat article reached the top of HN but was penalized so heavily at 8:22 am that it dropped off the chart entirely.
Why you should never use MongoDB was hugely popular and would have spent much of the day in the #1 spot, except it was rapidly penalized and languished around #7.
Severing ties with the NSA started off with a NSA penalty but was so hugely popular it still got the #1 spot. However, it was quickly given an even bigger penalty, forcing it down the page. Finally, near the end of the day $4.1m goes missing was penalized. As it turns out, it would have soon lost the #1 spot to FTL even without the penalty.
The green triangles and text show where "controversy" penalties were applied. The blue triangles and text show where articles were penalized into oblivion, dropping off the top 60. Milder penalties are not shown here.
It's clear that the content of the #1 spot on HN isn't "natural", but results from the constant application of penalties to many articles. It's unclear if these penalties result from HN administrators or from flagged articles.
This chart shows a few interesting things. The score for an article shoots up rapidly and then slowly drops over many hours. The scoring formula accounts for much of this: an article getting a constant rate of votes will peak quickly and then gradually descend. But the observed peak is even faster - this is because articles tend to get a lot of votes in the first hour or two, and then the voting rate drops off. Combining these two factors yields the steep curves shown.
There are a few articles each day that score much above the rest, along with a lot of articles in the middle. Some articles score very well but are unlucky and get stuck behind a more popular article. Other articles hit #1 briefly, between the fall of one and the climb of another.
Looking at the difference between the article with the top raw score (top of the graph) and the top-ranked article (red line), you can see when penalties have been applied.
The article Getting website registration completely wrong hit #1 early in the morning, but was penalized for controversy and rapidly dropped down the page, letting Linux ate my RAM briefly get the #1 spot before Simpsons in CSS overtook it.
A bit later, the controversy penalty was applied to Apple Maps shortly after it reached the #1 spot, causing it to lose its #1 spot and rapidly drop down the rankings.
The Snapchat article reached the top of HN but was penalized so heavily at 8:22 am that it dropped off the chart entirely.
Why you should never use MongoDB was hugely popular and would have spent much of the day in the #1 spot, except it was rapidly penalized and languished around #7.
Severing ties with the NSA started off with a NSA penalty but was so hugely popular it still got the #1 spot. However, it was quickly given an even bigger penalty, forcing it down the page. Finally, near the end of the day $4.1m goes missing was penalized. As it turns out, it would have soon lost the #1 spot to FTL even without the penalty.
The green triangles and text show where "controversy" penalties were applied. The blue triangles and text show where articles were penalized into oblivion, dropping off the top 60. Milder penalties are not shown here.
It's clear that the content of the #1 spot on HN isn't "natural", but results from the constant application of penalties to many articles. It's unclear if these penalties result from HN administrators or from flagged articles.
Submissions that get automatically penalized
Some submissions get automatically penalized based on the title, and others get penalized based on the domain. It appears that any article with NSA in the title gets an automatic penalty of .4. I looked for other words causing automatic penalties, such as awesome, bitcoin, and bubble but they do not seem to get penalized. I observed that many websites appear to automatically get a penalty of .25 to .8: arstechnica.com, businessinsider.com, easypost.com, github.com, imgur.com, medium.com, quora.com, qz.com, reddit.com, rt.com, stackexchange.com, theguardian.com, theregister.com, theverge.com, torrentfreak.com, youtube.com. I'm sure the actual list is longer. (This is separate from "banned" sites, which were listed at one point. One interesting theory by eterm is that news from popular sources gets submitted in parallel by multiple people resulting in more upvotes than the article "merits". Automatically penalizing popular websites would help counteract this effect.The impact of penalties
Using the scoring formula, the impact of a penalty can be computed. If an article gets a penalty factor of .4, this is equivalent to each vote only counting as .3 votes. Alternatively, the article will drop in ranking 66% faster than normal. A penalty factor of .1 corresponds to each vote counting as .05 votes, or the article dropping at 3.6 times the normal rate. Thus, a penalty factor of .4 has a significant impact, and .1 is very severe.
Controversy
In order to prevent flamewars on Hacker News, articles with "too many" comments will get heavily penalized as "controversial".
In the published code, the contro-factor function kicks in for any post with more than 20 comments and more comments than upvotes. Such an article is scaled by (votes/comments)^2. However, the actual formula is different - it is active for any post with more comments than upvotes and at least 40 comments. Based on empirical data, I suspect the exponent is 3, rather than 2 but haven't proven this.
The controversy penalty can have a sudden and catastrophic effect on an article's ranking, causing an article to be ranked highly one minute and vanish when it hits 40 comments. If you've wondered why a popular article suddenly vanishes from the front page, controversy is a likely cause.
For example,
Why the Chromebook pundits are out of touch with reality dropped from #5 to #22 the moment it hit 40 comments, and
Show HN: Get your health records from any doctor' was at #17 but vanished from the top 60 entirely on hitting 40 comments.
My methodology
I crawled the/news and /news2 pages every minute (staying under the 2 pages per minute guideline). I parsed the (somewhat ugly) HTML with Beautiful Soup, processed the results with a big pile of Python scripts, and graphed results with the incomprehensible but powerful matplotlib.
The basic idea behind the analysis is to generate raw scores using the formula and then look for anomalies. At a point in time (e.g. 11/09 8:46), we can compute the raw scores on the top 10 stories:
2.802 Pyret: A new programming language from the creators of Racket 1.407 The Big Data Brain Drain: Why Science is in Trouble 1.649 The NY Times endorsed a secretive trade agreement that the public can't read 0.785 S.F. programmers build alternative to HealthCare.gov (warning: autoplay video) 0.844 Marelle: logic programming for devops 0.738 Sprite Lamp 0.714 Why Teenagers Are Fleeing Facebook 0.659 NodeKnockout is in Full Tilt. Checkout some demos 0.805 ISO 1 0.483 Shopify accepts Bitcoin. 0.452 Show HN: Understand closuresNote that three of the top 10 articles are ranked lower than expected from their score: The NY Times, Marelle and ISO 1. Since The NY Times is ranked between articles with 1.407 and 0.785, its penalty factor can be computed as between .47 and .85. Likewise, the other penalties must be .87 to .93, and .60 to .82. I observed that most stories are ranked according to their score, and the exceptions are consistently ranked much lower, indicating a penalty. This indicates that the scoring formula in use matches the published code. If the formula were different, for instance the gravity exponent were larger, I'd expect to see stories drift out of their "expected" ranking as their votes or age increased, but I never saw this. This technique shows the existence of a penalty and gives a range for the penalty, but determining the exact penalty is difficult. You can look at the range over time and hope that it converges to a single value. However, several sources of error mess this up. First, the neighboring articles may also have penalties applied, or be scored differently (e.g. job postings). Second, because articles are not constantly reranked, an article may be out of place temporarily. Third, the penalty on an article may change over time. Fourth, the reported vote count may differ from the actual vote count because "bad" votes get suppressed. The result is that I've been able to determine approximate penalties, but there is a fair bit of numerical instability.
Penalties over a day
The following graph shows the calculated penalties over the course of a day. Each line shows a particular article. It should start off at 1 (no penalty), and then drop to a penalty level when a penalty is applied. The line ends when the article drops off the top 60, which can be fairly soon after the penalty is applied. There seem to be penalties of 0.2 and 0.4, as well as a lot in the 0.8-0.9 range. It looks like a lot of penalties are applied at 9am (when moderators arrive?), with more throughout the day. I'm experimenting with different algorithms to improve the graph since it is pretty noisy.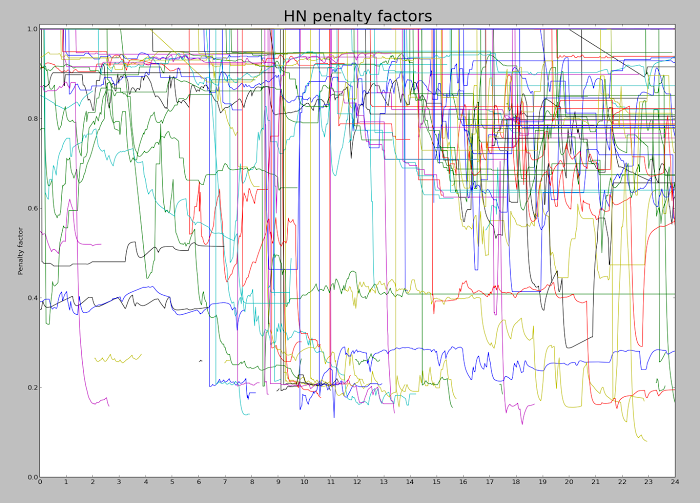
On average, about 20% of the articles on the front page have been penalized, while 38% of the articles on the second page have been penalized. (The front page rate is lower since penalized articles are less likely to be on the front page, kind of by definition.) There is a lot more penalization going on than you might expect. Here's a list of the articles on the front page on 11/11 that were penalized. (This excludes articles that would have been there if they weren't penalized.) This list is much longer than I expected; scroll for the full list.
The code for the scoring formula
The Arc source code for a version of the HN server is available, as well as an updated scoring formula: (= gravity* 1.8 timebase* 120 front-threshold* 1
nourl-factor* .4 lightweight-factor* .17 gag-factor* .1)
(def frontpage-rank (s (o scorefn realscore) (o gravity gravity*))
(* (/ (let base (- (scorefn s) 1)
(if (> base 0) (expt base .8) base))
(expt (/ (+ (item-age s) timebase*) 60) gravity))
(if (no (in s!type 'story 'poll)) .8
(blank s!url) nourl-factor*
(mem 'bury s!keys) .001
(* (contro-factor s)
(if (mem 'gag s!keys)
gag-factor*
(lightweight s)
lightweight-factor*
1)))))
In case you don't read Arc code, the above snippet defines several constants: gravity* = 1.8, timebase* = 120 (minutes), etc. It then defines a method frontpage-rank that ranks a story s based on its upvotes (realscore) and age in minutes (item-age).
The penalty factor is defined by an if with several cases. If the article is not a 'story' or 'poll', the penalty factor is .8. Otherwise, if the URL field is blank (Ask HN, etc.) the factor is nourl-factor*. If the story has been flagged as 'bury', the scale factor is 0.001 and the article is ranked into oblivion. Finally, the default case combines the controversy factor and the gag/lightweight factor.
The controversy factor contro-factor is intended to suppress articles that are leading to flamewars, and is discussed more later.
The next factor hits an article flagged as a gag (joke) with a heavy value of .1, and a "lightweight" article with a factor of .17. The actual penalty system appears to be much more complex than what appears in the published code.
Conclusion
An article's position on the Hacker News home page isn't the meritocracy based on upvotes that you might expect. By carefully examining the articles that appear on the Hacker News page, we can learn a great deal about the scoring formula in use. While upvotes are the obvious factor controlling rankings, there is also a complex "penalty" system causing articles to be ranked lower or disappear entirely. This isn't just preventing spam, but affects many very popular articles. And if an article has more comments than votes, don't add your comment to it or you may kill it off entirely! See discussion on Hacker News.Update (11/18): article on penalties is penalized
Ironically, this article was penalized on Hacker News. Minutes after reaching the front page, a heavy 0.2 penalty was applied to the article, forcing it off the front page. The black line in the graph below shows the position of this article on Hacker News. You can see the sharp drop when the penalty was applied. The gray line shows where the article would have been ranked without the penalty. Without the penalty, the article would have been in the #5 spot, but with the penalty it never made it back onto the front page (positions 1-30). The lower green line shows the raw score of this article. (11/26: I'm told that the penalty was because the "voting ring detection" triggered erroneously.)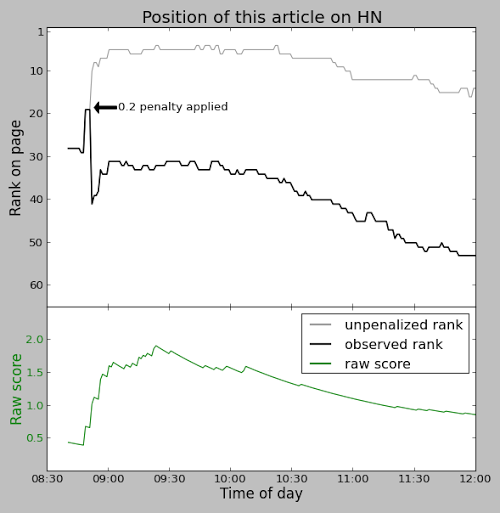
 I've been experimenting with IPv6 on my home network. In
I've been experimenting with IPv6 on my home network. In